Clustering of scikit-learn toy data sets¶
Go to:
CommonNN clustering using …
Notebook configuration¶
[1]:
import sys
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import sklearn
from sklearn import datasets
from sklearn.metrics import pairwise_distances
from sklearn.neighbors import KDTree
from sklearn.preprocessing import StandardScaler
import commonnn
from commonnn import cluster
from commonnn import _types, _fit
[2]:
# Helper function definitions
def indent_at_parens(s):
"""Take a string and introduce indention at parentheses"""
o = ""
level = 1
saw_comma = False
for c in s:
if saw_comma:
if c == " ":
o += f"\n{' ' * (level - 1)}"
else:
o += f"\n{' ' * (level - 1)}{c}"
saw_comma = False
continue
if c == "(":
o += f"(\n{' ' * level}"
level += 1
continue
if c == ")":
level -= 1
o += f"\n{' ' * level})"
continue
if c == ",":
saw_comma = True
o += ","
continue
o += c
return o
Print Python and package version information:
[3]:
# Version information
print("Python: ", *sys.version.split("\n"))
print("Packages:")
for package in [mpl, np, sklearn, commonnn]:
print(f" {package.__name__}: {package.__version__}")
Python: 3.9.0 | packaged by conda-forge | (default, Nov 26 2020, 07:57:39) [GCC 9.3.0]
Packages:
matplotlib: 3.9.4
numpy: 1.26.4
sklearn: 1.6.1
commonnn: 0.0.3
We use Matplotlib to create plots. The matplotlibrc file in the root directory of the CommonNNClustering repository is used to customize the appearance of the plots.
[4]:
# Matplotlib configuration
mpl.rc_file(
"../../matplotlibrc",
use_default_template=False
)
[5]:
# Axis property defaults for the plots
ax_props = {
"xlabel": None,
"ylabel": None,
"xlim": (-2.5, 2.5),
"ylim": (-2.5, 2.5),
"xticks": (),
"yticks": (),
"aspect": "equal"
}
# Line plot property defaults
line_props = {
"linewidth": 0,
"marker": '.',
}
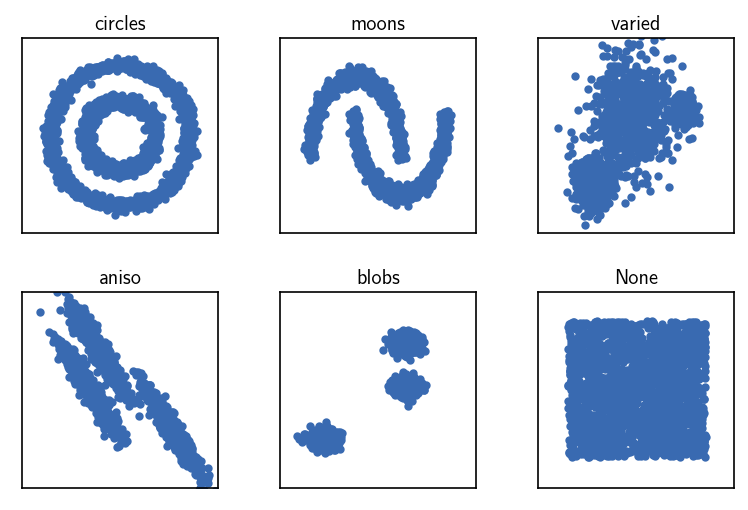
Data set generation¶
To see the common-nearest-neighbours (CommonNN) clustering in action, let’s have a look at a handful of basic 2D data sets from scikit-learn (like here in the scikit-learn documentation). We will cluster the data sets starting from different input data formats using the provided defaults. For more details see also the Advanced usage tutorial.
[6]:
# Data set generation parameters
np.random.seed(0)
n_samples = 2000
[7]:
# Data set generation
# Fit all datasets to the same value range
# using `data = StandardScaler().fit_transform(data)`
# circles
noisy_circles, _ = datasets.make_circles(
n_samples=n_samples,
factor=.5,
noise=.05
)
noisy_circles = StandardScaler().fit_transform(noisy_circles)
# moons
noisy_moons, _ = datasets.make_moons(
n_samples=n_samples,
noise=.05
)
noisy_moons = StandardScaler().fit_transform(noisy_moons)
# blobs
blobs, _ = datasets.make_blobs(
n_samples=n_samples,
random_state=8
)
blobs = StandardScaler().fit_transform(blobs)
# None
no_structure = np.random.rand(
n_samples, 2
)
no_structure = StandardScaler().fit_transform(no_structure)
# aniso
random_state = 170
X, y = datasets.make_blobs(
n_samples=n_samples,
random_state=random_state
)
transformation = [[0.6, -0.6], [-0.4, 0.8]]
aniso = np.dot(X, transformation)
aniso = StandardScaler().fit_transform(aniso)
# varied
varied, _ = datasets.make_blobs(
n_samples=n_samples,
cluster_std=[1.0, 2.5, 0.5],
random_state=random_state
)
varied = StandardScaler().fit_transform(varied)
[8]:
# Define cluster parameters
dsets = [ # "name", set, **parameters
('circles', noisy_circles, {
'radius_cutoff': 0.5,
'similarity_cutoff': 20,
'member_cutoff': 100,
'max_clusters': None
}),
('moons', noisy_moons, {
'radius_cutoff': 0.5,
'similarity_cutoff': 20,
'member_cutoff': 2,
'max_clusters': None
}),
('varied', varied, {
'radius_cutoff': 0.28,
'similarity_cutoff': 20,
'member_cutoff': 20,
'max_clusters': None
}),
('aniso', aniso, {
'radius_cutoff': 0.29,
'similarity_cutoff': 30,
'member_cutoff': 5,
'max_clusters': None
}),
('blobs', blobs, {
'radius_cutoff': 0.4,
'similarity_cutoff': 20,
'member_cutoff': 2,
'max_clusters': None
}),
('None', no_structure, {
'radius_cutoff': 0.5,
'similarity_cutoff': 20,
'member_cutoff': 1,
'max_clusters': None
}),
]
[9]:
# Plot the original data sets
fig, ax = plt.subplots(2, 3)
Ax = ax.flatten()
for count, (name, data, *_) in enumerate(dsets):
Ax[count].plot(data[:, 0], data[:, 1], **line_props)
Ax[count].set(**ax_props)
Ax[count].set_title(f'{name}', fontsize=10, pad=4)
fig.subplots_adjust(
left=0, right=1, bottom=0, top=1, wspace=0.1, hspace=0.3
)
CommonNN clustering using data point coordinates as input¶
[10]:
fig, ax = plt.subplots(2, 3)
Ax = ax.flatten()
for count, (name, data, params) in enumerate(dsets):
# Default clustering initialisation
clustering = cluster.Clustering(data)
# Calculate neighbours brute force
clustering.fit(**params)
print()
clustering.evaluate(ax=Ax[count], annotate_pos="random")
Ax[count].set(**ax_props)
Ax[count].set_title(f'{name}', fontsize=10, pad=4)
fig.subplots_adjust(
left=0, right=1, bottom=0, top=1, wspace=0.1, hspace=0.3
)
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.500 20 100 None 2 0.500 0.000 00:00:0.086
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.500 20 2 None 2 0.500 0.000 00:00:0.094
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.280 20 20 None 3 0.338 0.114 00:00:0.126
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.290 30 5 None 3 0.319 0.050 00:00:0.099
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.400 20 2 None 3 0.334 0.001 00:00:0.149
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.500 20 1 None 1 1.000 0.000 00:00:0.084
-----------------------------------------------------------------------------------------------

When raw input data is presented to a Clustering on creation without specifying anything else, the obtained Clustering object aggregates the needed clustering components, assuming that it got point coordinates as a sequence of sequences. The neighbourhood of a specific point will be collected brute-force by computing the (Euclidean) distances to all other points and comparing them to the radius cutoff. This will be the slowest possible approach but it has fairly conservative memory
usage.
[11]:
# Clustering components used by default ("coordinates" recipe)
print(indent_at_parens(str(clustering)))
Clustering(
input_data=InputDataExtComponentsMemoryview(
components of 2000 points in 2 dimensions
),
fitter=FitterExtCommonNNBFS(
ngetter=NeighboursGetterExtBruteForce(
dgetter=DistanceGetterExtMetric(
metric=MetricExtEuclideanReduced
),
sorted=False,
selfcounting=True
),
na=NeighboursExtVectorUnorderedSet,
nb=NeighboursExtVectorUnorderedSet,
checker=SimilarityCheckerExtSwitchContains,
queue=QueueExtFIFOQueue
),
hierarchical_fitter=None,
predictor=None
)
CommonNN clustering with pre-computed distances¶
[12]:
fig, ax = plt.subplots(2, 3)
Ax = ax.flatten()
for count, (name, data, params) in enumerate(dsets):
# Default clustering initialisation
clustering = cluster.Clustering(data)
# Pre-compute distances and choose the corresponding recipe
distances = pairwise_distances(data)
clustering_dist = cluster.Clustering(
distances,
recipe="distances"
)
# Use pre-computed distances
clustering_dist.fit(**params)
clustering.labels = clustering_dist.labels
print()
clustering.evaluate(ax=Ax[count], annotate_pos="random")
Ax[count].set(**ax_props)
Ax[count].set_title(f'{name}', fontsize=10, pad=4)
fig.subplots_adjust(
left=0, right=1, bottom=0, top=1, wspace=0.1, hspace=0.3
)
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.500 20 100 None 2 0.500 0.000 00:00:0.116
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.500 20 2 None 2 0.500 0.000 00:00:0.105
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.280 20 20 None 3 0.338 0.114 00:00:0.128
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.290 30 5 None 3 0.319 0.050 00:00:0.136
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.400 20 2 None 3 0.334 0.001 00:00:0.166
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.500 20 1 None 1 1.000 0.000 00:00:0.101
-----------------------------------------------------------------------------------------------

When raw input data is presented to a Clustering on creation in terms of a dense distance matrix, the “distances” recipe can be chosen to make the obtained Clustering object aggregate the needed clustering components. The neighbourhood of a specific point will be collected brute-force by looking up distances from the input data. This will be somewhat faster as no distances need to be calculated during the clustering but it has a high memory demand. It also allows to leverage smart
external methods for the task of the distance calculation.
[13]:
# Clustering components used by the "distance" recipe
print(indent_at_parens(str(clustering_dist)))
Clustering(
input_data=InputDataExtComponentsMemoryview(
components of 2000 points in 2000 dimensions
),
fitter=FitterExtCommonNNBFS(
ngetter=NeighboursGetterExtBruteForce(
dgetter=DistanceGetterExtMetric(
metric=MetricExtPrecomputed
),
sorted=False,
selfcounting=True
),
na=NeighboursExtVectorUnorderedSet,
nb=NeighboursExtVectorUnorderedSet,
checker=SimilarityCheckerExtSwitchContains,
queue=QueueExtFIFOQueue
),
hierarchical_fitter=None,
predictor=None
)
CommonNN clustering with pre-computed neighbourhoods¶
[14]:
fig, ax = plt.subplots(2, 3)
Ax = ax.flatten()
for count, (name, data, params) in enumerate(dsets):
clustering = cluster.Clustering(data)
# Pre-compute neighbourhoods and choose the corresponding recipe
tree = KDTree(data)
neighbourhoods = tree.query_radius(
data, r=params["radius_cutoff"], return_distance=False
)
clustering_neighbourhoods = cluster.Clustering(
neighbourhoods,
recipe="neighbourhoods"
)
# Use pre-computed neighbourhoods
clustering_neighbourhoods.fit(**params)
clustering.labels = clustering_neighbourhoods.labels
print()
clustering.evaluate(ax=Ax[count], annotate_pos="random")
Ax[count].set(**ax_props)
Ax[count].set_title(f'{name}', fontsize=10, pad=4)
fig.subplots_adjust(
left=0, right=1, bottom=0, top=1, wspace=0.1, hspace=0.3
)
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.500 20 100 None 2 0.500 0.000 00:00:0.015
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.500 20 2 None 2 0.500 0.000 00:00:0.021
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.280 20 20 None 3 0.338 0.114 00:00:0.026
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.290 30 5 None 3 0.319 0.050 00:00:0.018
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.400 20 2 None 3 0.334 0.001 00:00:0.064
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.500 20 1 None 1 1.000 0.000 00:00:0.014
-----------------------------------------------------------------------------------------------

When raw input data is presented to a Clustering on creation in terms of pre-computed neighbourhoods, the “neighbourhoods” recipe can be chosen to make the obtained Clustering object aggregate the needed clustering components. The neighbourhood of a specific point will looked up from the input data. This will be considerably faster and it has a lower memory demand compared to the “distances” case. It also allows to leverage smart external methods for the task of the neighbourhood
calculation.
Note, that the “neighbourhoods” recipe requires the raw neighbourhoods in the concrete format of a matrix in which the neighbourhoods of individual points are padded to the length of the largest neighbourhood. If neighbourhoods are presented in terms of a sequence of sequences (with varying length) as one would get from a tree query to sklearn.neighbors.KDTree, this can be transformed into the suitable format using the preparation hook hooks.prepare_neighbourhoods.
[15]:
# Clustering components used by the "distance" recipe
print(indent_at_parens(str(clustering_neighbourhoods)))
Clustering(
input_data=InputDataExtNeighbourhoodsMemoryview(
neighbourhoods of 2000 points
),
fitter=FitterExtCommonNNBFS(
ngetter=NeighboursGetterExtLookup(
sorted=False,
selfcounting=True
),
na=NeighboursExtVectorUnorderedSet,
nb=NeighboursExtVectorUnorderedSet,
checker=SimilarityCheckerExtSwitchContains,
queue=QueueExtFIFOQueue
),
hierarchical_fitter=None,
predictor=None
)
CommonNN clustering with pre-computed neighbourhoods (sorted by member index)¶
[16]:
fig, ax = plt.subplots(2, 3)
Ax = ax.flatten()
for count, (name, data, params) in enumerate(dsets):
clustering = cluster.Clustering(data)
# Pre-compute and sort neighbourhoods and choose the corresponding recipe
tree = KDTree(data)
neighbourhoods = tree.query_radius(
data, r=params["radius_cutoff"], return_distance=False
)
for n in neighbourhoods:
n.sort()
# Custom initialisation using a clustering builder
clustering_neighbourhoods_sorted = cluster.Clustering(
neighbourhoods,
recipe="sorted_neighbourhoods"
)
# Use pre-computed neighbourhoods
clustering_neighbourhoods_sorted.fit(**params)
clustering.labels = clustering_neighbourhoods_sorted.labels
print()
clustering.evaluate(ax=Ax[count], annotate_pos="random")
Ax[count].set(**ax_props)
Ax[count].set_title(f'{name}', fontsize=10, pad=4)
fig.subplots_adjust(
left=0, right=1, bottom=0, top=1, wspace=0.1, hspace=0.3
)
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.500 20 100 None 2 0.500 0.000 00:00:0.003
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.500 20 2 None 2 0.500 0.000 00:00:0.003
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.280 20 20 None 3 0.338 0.114 00:00:0.005
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.290 30 5 None 3 0.319 0.050 00:00:0.003
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.400 20 2 None 3 0.334 0.001 00:00:0.009
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.500 20 1 None 1 1.000 0.000 00:00:0.003
-----------------------------------------------------------------------------------------------

Pre-computed neighbourhood information can be additionally sorted in terms of the indices of the members (i.e. so that within each neighbourhood the members are stored in increasing order of there index in the data set). While this has the same memory demand as using unsorted neighbourhoods, it offers the fastest clustering.
[17]:
# Clustering components used by the "distance" recipe
print(indent_at_parens(str(clustering_neighbourhoods_sorted)))
Clustering(
input_data=InputDataExtNeighbourhoodsMemoryview(
neighbourhoods of 2000 points
),
fitter=FitterExtCommonNNBFS(
ngetter=NeighboursGetterExtLookup(
sorted=True,
selfcounting=True
),
na=NeighboursExtVector,
nb=NeighboursExtVector,
checker=SimilarityCheckerExtScreensorted,
queue=QueueExtFIFOQueue
),
hierarchical_fitter=None,
predictor=None
)
CommonNN clustering with pre-computed neighbourhoods (sorted by member index and neighbour count)¶
[19]:
fig, ax = plt.subplots(2, 3)
Ax = ax.flatten()
for count, (name, data, params) in enumerate(dsets):
clustering = cluster.Clustering(data)
# Pre-compute and sort neighbourhoods and choose the corresponding recipe
tree = KDTree(data)
neighbourhoods = tree.query_radius(
data, r=params["radius_cutoff"], return_distance=False
)
n_members = np.array([
n.shape[0]
for n in neighbourhoods
])
sorted_by_member_count = np.argsort(n_members)[::-1]
revert_sort = np.argsort(sorted_by_member_count)
neighbourhoods = neighbourhoods[sorted_by_member_count]
neighbourhoods = [revert_sort[n] for n in neighbourhoods]
for n in neighbourhoods:
n.sort()
# Custom initialisation using a clustering builder
clustering_neighbourhoods_sorted = cluster.Clustering(
neighbourhoods,
recipe="sorted_neighbourhoods"
)
# Use pre-computed neighbourhoods
clustering_neighbourhoods_sorted.fit(**params)
clustering.labels = clustering_neighbourhoods_sorted.labels[revert_sort]
print()
clustering.evaluate(ax=Ax[count], annotate_pos="random")
Ax[count].set(**ax_props)
Ax[count].set_title(f'{name}', fontsize=10, pad=4)
fig.subplots_adjust(
left=0, right=1, bottom=0, top=1, wspace=0.1, hspace=0.3
)
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.500 20 100 None 2 0.500 0.000 00:00:0.002
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.500 20 2 None 2 0.500 0.000 00:00:0.003
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.280 20 20 None 3 0.338 0.114 00:00:0.004
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.290 30 5 None 3 0.319 0.050 00:00:0.003
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.400 20 2 None 3 0.334 0.001 00:00:0.009
-----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
#points r nc min max #clusters %largest %noise time
2000 0.500 20 1 None 1 1.000 0.000 00:00:0.003
-----------------------------------------------------------------------------------------------

As a further addition to the sorting of each neighbourhood by member indices, it is possible to sort all neighbourhoods according to their member count (i.e. so that the point with the highest neighbour count becomes the first point in the data set). It is not guaranteed but this additional sorting can make the clustering even more efficient.
[20]:
# Clustering components used by the "distance" recipe
print(indent_at_parens(str(clustering_neighbourhoods_sorted)))
Clustering(
input_data=InputDataExtNeighbourhoodsMemoryview(
neighbourhoods of 2000 points
),
fitter=FitterExtCommonNNBFS(
ngetter=NeighboursGetterExtLookup(
sorted=True,
selfcounting=True
),
na=NeighboursExtVector,
nb=NeighboursExtVector,
checker=SimilarityCheckerExtScreensorted,
queue=QueueExtFIFOQueue
),
hierarchical_fitter=None,
predictor=None
)